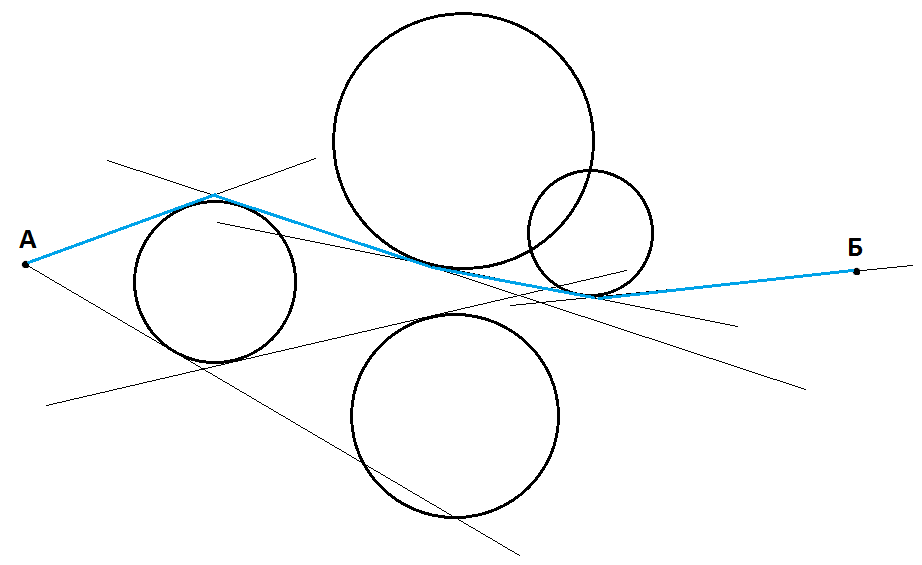
- На плоском пространстве есть огромное число окружностей двух типов:
а) непроходимые
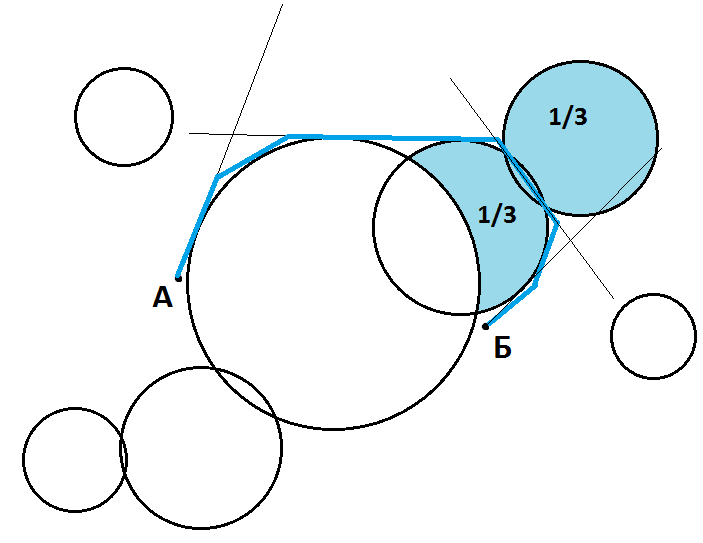
б) замедляют движение в 3 раза внутри себя
- Окружности не постоянны, т.е. могут возникать или исчезать со временем (вариант с левел-дизайнером и ручным построением графа для A* отпадает)
- Окружности могут пересекаться.
- Окружности имеют любой радиус, как маленький, так и очень большой.
- Персонаж представляет безразмерную точку.
- Все размеры (координаты, радиусы) - вещественные.
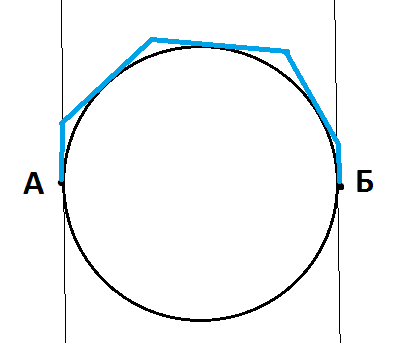
Как для конкретного момента времени найти почти оптимальный путь из точки А в точку Б, состоящий из отрезков (ломаная линия)?